


The Least Squares Regression Calculator is biased against data points On the same note, the linear regression process is very sensitive to.Trying too hard to fit a model to a pre-conceived trend. The R-squared metric isn't perfect, but can alert you to when you are.Keep this in mind when you use the Least Squares Regression Calculator - are you fitting the correct curve? Not the case many engineering and social systems are driven by different dynamics better represented by exponential, polynomial, or power models. You are modeling behaves according to a linear system. Using a linear model assumes the underlying process.Both of theseĬan bias the training sample away from the true population dynamics. Same individual multiple times (for medical studies). You risk stumbling across unrepresented (or under-represented) groups.Ĭlustering across time is another pitfall - where you re-measure the You attempt to use the model on populations outside the training set, The model can't predict behavior it cannot seeĪnd assumes the sample is representative of the total population. The first - clustering in the same space - is a function ofĬonvenience sampling. Data observations must be truly independent.This is important if you're concerned with a small subset of the population, where extreme values trigger extreme outcomes. The modeling process only looks at the mean of theĭependent variable.Some practical comments on real world analysis: The points are from the calculated least squares regression line. You an estimate of the error associated with effort: how far Particular interest since you can use it to predict points That specific value of X.The equation of the line is of The chart (in most browsers), you can get a predicted Y value for
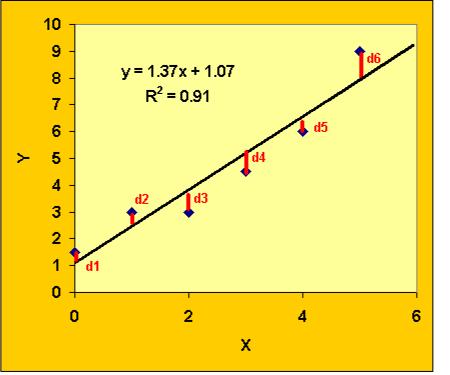
To help you visualize the trend - we display a plot of theĭata and the trend-line we fit through it. For a deeper view of the mathematicsīehind the approach, here's a regression tutorial. It will also generate an R-squared statistic, which evaluates howĬlosely variation in the independent variable matches variation in theĭependent variable (the outcome). The Least Squares Regression Calculator will return the slope of the line and the y-intercept. Predicted value of the dependent variable and the actual value. Trend-line to your data, seeking to avoid large gaps between the This linear regression calculator fits a trend-line to your data using the Interpreting The Least Squares Regression Calculator Results To retrieve it,Īll you need to do is click the "load data" button next to it. Saved datasets below the data entry panel. It will save the data in your browser (not on our You can save your data for use with this webpage and the To give you a perspective on fit & accuracy. Tool can also serve as a sum of squared residuals calculator Measuring the relationship between the two factors.
It can serve as a slope of regression line calculator, Will generate the parameters of the line for your analysis. This page includes a regression equation calculator, which The slope and intercept of a trendline that is the best fit The linear regression calculator will estimate Enter each data point as a separate line. This is a online regression calculator for statistical use.Įnter your data as a string of number pairs, separated byĬommas. We already have the train set and test set, now we have to build the Regression Model.How To Use The Least Squares Regression Calculator If we leave it blank or 0, the RandomState instance used by np.random will be used instead. We can put an instance of the RandomState class as well. random_state: this is the seed for the random number generator.train_size: if we use the test_size already, the rest of data will automatically be assigned to train_size.Normally, we should pick around 5% to 30%. We should not let the test set too big if it’s too big, we will lack of data to train. You can put it 1/5 to get 20% or 0.2, they are the same. test_size=0.2: we will split our dataset (10 observations) into 2 parts (training set, test set) and the ratio of test set compare to dataset is 0.2 (2 observations will be put into the test set.


 0 kommentar(er)
0 kommentar(er)
